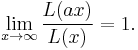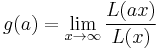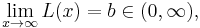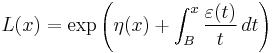Slowly varying function

In real analysis, a branch of mathematics, a slowly varying function is a function resembling a function converging at infinity. A regularly varying function resembles a power law function near infinity. Slowly varying and regularly varying functions are important in probability theory.

Contents 1 Definition 2 Examples 3 Properties 4 References

Definition

A function L: (0,∞) → (0, ∞) is called slowly varying (at infinity) if for all a > 0,

If the limit

is finite but nonzero for every a > 0, the function L is called a regularly varying function.

These definitions are due to Jovan Karamata (Galambos & Seneta 1973). Regular variation is the subject of (Bingham, Goldie & Teugels 1989)

Examples

• If L has a limit

then L is a slowly varying function.

• For any β∈R, the function L(x)= log^β x is slowly varying.
• The function L(x)=x is not slowly varying, neither is L(x)=x^β for any real β;≠0. However, they are regularly varying.

Properties

Some important properties are (Galambos & Seneta 1973):

• The limit in the definition is uniform if a is restricted to a finite interval.
• Karamata's characterization theorem: every regularly varying function is of the form x ^βL(x) where β ≥ 0 and L is a slowly varying function. That is, the function g(a) in the definition has to be of the form λ^ρ; the number ρ is called the index of regular variation.
• Representation theorem: a function L is slowly varying if and only if there exists B > 0 such that for all x ≥ B the function can be written in the form

where η(x) converges to a finite number and ε(x) converges to zero as x goes to infinity, and both functions are measurable and bounded.

References

• Bingham, N.H. (2001), "Slowly varying function", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=k/k110030 

• Bingham, N.H.; Goldie, C.M.; Teugels, J.L. (1989), Regular Variation, Cambridge University Press .

• Galambos, J.; Seneta, E. (1973), "Regularly Varying Sequences", Proceedings of the American Mathematical Society 41 (1): 110–116, doi:10.2307/2038824, ISSN 0002-9939, JSTOR 2038824 .